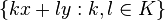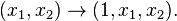These parallel lines appear to intersect in the vanishing point "at infinity". In a projective plane this is actually true.

In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that do not intersect. A projective plane can be thought of as an ordinary plane equipped with additional "points at infinity" where parallel lines intersect. Thus any two lines in a projective plane intersect in one and only one point.

Renaissance artists, in developing the techniques of drawing in perspective, laid the groundwork for this mathematical topic. The archetypical example is the real projective plane, also known as the extended Euclidean plane.^[1] This example, in slightly different guises, is important in algebraic geometry,topology and projective geometry where it may be denoted variously by PG(2, R), RP², or P₂(R) among other notations. There are many other projective planes, both infinite, such as the complex projective plane, and finite, such as the Fano plane.

A projective plane is a 2-dimensional projective space, but not all projective planes can be embedded in 3-dimensional projective spaces. The embedding property is a consequence of a result known asDesargues' theorem.

Definition[edit]

A projective plane consists of a set of lines, a set of points, and a relation between points and lines called incidence, having the following properties:^[2]

The second condition means that there are no parallel lines. The last condition excludes the so-called degenerate cases (see below). The term "incidence" is used to emphasize the symmetric nature of the relationship between points and lines. Thus the expression "point P is incident with line l " is used instead of either "P is on l " or "l passes through P ".

Some examples[edit]

The extended Euclidean plane[edit]

To turn the ordinary Euclidean plane into a projective plane proceed as follows:

1. To each class of parallel lines add a single new point. That point is considered incident with each line of the class. Different parallel classes get different points. These points are called points at infinity.
2. Add a new line which is considered incident with all the points at infinity (and only them). This line is called the line at infinity.

The extended structure is a projective plane and is called the Extended Euclidean Plane or the real projective plane. The process outlined above, used to obtain it, is called "projective completion" or projectivization. This plane can also be constructed by starting from R³ viewed as a vector space, see below.

Projective Moulton Plane[edit]

 

The Moulton plane. Lines sloping down and to the right are bent where they cross the y-axis.

The points of the Moulton plane are the points of the Euclidean plane, with coordinates in the usual way. To create the Moulton plane from the Euclidean plane some of the lines are redefined. That is, some of their point sets will be changed, but other lines will remain unchanged. Redefine all the lines with negative slopes so that they look like "bent" lines, meaning that these lines keep their points with negative x-coordinates, but the rest of their points are replaced with the points of the line with the same y-intercept but twice the slope wherever their x-coordinate is positive.

The Moulton plane has parallel classes of lines and is an affine plane. It can be projectivized, as in the previous example, to obtain the projective Moulton Plane.Desargues' Theorem is not a valid theorem in either the Moulton plane or the projective Moulton plane.

A finite example[edit]

This example has just thirteen points and thirteen lines. We label the points P₁,...,P₁₃ and the lines m₁,...,m₁₃. The incidence relation (which points are on which lines) can be given by the following incidence matrix. The rows are labelled by the points and the columns are labelled by the lines. A 1 in row i and column j means that the point P_i is on the line m_j, while a 0 (which we represent here by a blank cell for ease of reading) means that they are not incident. The matrix is in Paige-Wexler normal form.

	m1	m2	m3	m4	m5	m6	m7	m8	m9	m10	m11	m12	m13
P1	1	1	1	1
P2	1				1	1	1
P3	1							1	1	1
P4	1										1	1	1
P5		1			1			1			1
P6		1				1			1			1
P7		1					1			1			1
P8			1		1				1				1
P9			1			1				1	1
P10			1				1	1				1
P11				1	1					1		1
P12				1		1		1					1
P13				1			1		1		1

To verify the conditions that make this a projective plane, observe that every two rows have exactly one common column in which 1's appear (every pair of distinct points are on exactly one common line) and that every two columns have exactly one common row in which 1's appear (every pair of distinct lines meet at exactly one point). Among many possibilities, the points P₁,P₄,P₅,and P₈, for example, will satisfy the third condition. This example is known as the projective plane of order three.

Vector space construction[edit]

Though the line at infinity of the extended real plane may appear to have a different nature than the other lines of that projective plane, this is not the case. Another construction of the same projective plane shows that no line can be distinguished (on geometrical grounds) from any other. In this construction, each "point" of the real projective plane is the one-dimensional subspace through the origin in a 3-dimensional vector space, and a "line" in the projective plane arises from a plane through the origin in the 3-space. This idea can be generalized and made more precise as follows.^[3]

Let K be any division ring (skewfield). Let K³ denote the set of all triples x = (x₀, x₁, x₂) of elements of K (a Cartesian product viewed as a vector space). For any nonzero x in K³, the minimal subspace of K³ containing x (which may be visualized as all the vectors in a line through the origin) is the subset

of K³. Similarly, let x and y be linearly independent elements of K³, meaning that kx + ly = 0 implies that k = l = 0. The minimal subspace of K³containing x and y (which may be visualized as all the vectors in a plane through the origin) is the subset

of K³. This 2-dimensional subspace contains various 1-dimensional subspaces through the origin that may be obtained by fixing k and l and taking the multiples of the resulting vector. Different choices of k and l that are in the same ratio will give the same line.

The projective plane over K, denoted PG(2,K) or KP², has a set of points consisting of all the 1-dimensional subspaces in K³. A subset L of the points of PG(2,K) is a line in PG(2,K) if there exists a 2-dimensional subspace of K³ whose set of 1-dimensional subspaces is exactly L.

Verifying that this construction produces a projective plane is usually left as a linear algebra exercise.

An alternate (algebraic) view of this construction is as follows. The points of this projective plane are the equivalence classes of the setK³ ∖ {(0, 0, 0)} modulo the equivalence relation

x ~ kx, for all k in K^×.

Lines in the projective plane are defined exactly as above.

The coordinates (x₀, x₁, x₂) of a point in PG(2,K) are called homogeneous coordinates. Each triple (x₀, x₁, x₂) represents a well-defined point in PG(2,K), except for the triple (0, 0, 0), which represents no point. Each point in PG(2,K), however, is represented by many triples.

If K is a topological space, then KP², inherits a topology via the product, subspace, and quotient topologies.

Classical examples[edit]

The real projective plane RP², arises when K is taken to be the real numbers, R. As a closed, non-orientable real 2-manifold, it serves as a fundamental example in topology.^[4]

In this construction consider the unit sphere centered at the origin in R³. Each of the R³ lines in this construction intersects the sphere at two antipodal points. Since the R³ line represents a point of RP², we will obtain the same model of RP² by identifying the antipodal points of the sphere. The lines of RP² will be the great circles of the sphere after this identification of antipodal points. This description gives the standard model of elliptic geometry.

The complex projective plane CP², arises when K is taken to be the complex numbers, C. It is a closed complex 2-manifold, and hence a closed, orientable real 4-manifold. It and projective planes over other fields (known as pappian planes) serve as fundamental examples inalgebraic geometry.^[5]

The quaternionic projective plane HP² is also of independent interest.^{[citation needed]}

Finite field planes[edit]

By Wedderburn's Theorem, a finite division ring must be commutative and so a field. Thus, the finite examples of this construction are known as "field planes". Taking K to be the finite field of q = pⁿ elements with prime p produces a projective plane of q² + q + 1 points. The field planes are usually denoted by PG(2,q) where PG stands for projective geometry, the "2" is the dimension and q is called the order of the plane (it is one less than the number of points on any line). The Fano plane, discussed below, is denoted by PG(2,2). The third example above is the projective plane PG(2,3).

 

The Fano plane. Points are shown as dots; lines are shown as lines or circles.

The Fano plane is the projective plane arising from the field of two elements. It is the smallest projective plane, with only seven points and seven lines. In the figure at right, the seven points are shown as small black balls, and the seven lines are shown as six line segments and a circle. However, one could equivalently consider the balls to be the "lines" and the line segments and circle to be the "points" – this is an example of duality in the projective plane: if the lines and points are interchanged, the result is still a projective plane (see below). A permutation of the seven points that carries collinear points (points on the same line) to collinear points is called a collineation or symmetry of the plane. The collineations of a geometry form a group under composition, and for the Fano plane this group (PΓL(3,2) = PGL(3,2)) has 168 elements.

Desargues' theorem and Desarguesian planes[edit]

The theorem of Desargues is universally valid in a projective plane if and only if the plane can be constructed from a three-dimensional vector space over a skewfield as above.^[6] These planes are called Desarguesian planes, named after Gérard Desargues. The real (or complex) projective plane and the projective plane of order 3 given above are examples of Desarguesian projective planes. The projective planes that can not be constructed in this manner are called non-Desarguesian planes, and the Moulton plane given above is an example of one. The PG(2,K) notation is reserved for the Desarguesian planes.

Subplanes[edit]

A subplane of a projective plane is a subset of the points of the plane which themselves form a projective plane with the same incidence relations.

(Bruck 1955) proves the following theorem. Let Π be a finite projective plane of order N with a proper subplane Π₀ of order M. Then either N =M² or N ≥ M² + M.

When N is a square, subplanes of order √N are called Baer subplanes. Every point of the plane lies on a line of a Baer subplane and every line of the plane contains a point of the Baer subplane.

In the finite Desarguesian planes PG(2,pⁿ), the subplanes have orders which are the orders of the subfields of the finite field GF(pⁿ), that is, pⁱwhere i is a divisor of n. In non-Desarguesian planes however, Bruck's theorem gives the only information about subplane orders. The case of equality in the inequality of this theorem is not known to occur. Whether or not there exists a subplane of order M in a plane of order N with M² +M = N is an open question. If such subplanes existed there would be projective planes of composite (non-prime power) order.

Fano subplanes[edit]

A Fano subplane is a subplane isomorphic to PG(2,2), the unique projective plane of order 2.

If you consider a quadrangle (a set of 4 points no three collinear) in this plane, the points determine six of the lines of the plane. The remaining three points (called the diagonal points of the quadrangle) are the points where the lines that do not intersect at a point of the quadrangle meet. The seventh line consists of all the diagonal points (usually drawn as a circle or semicircle).

The name Fano for this subplane is really a misnomer. Gino Fano (1871–1952), in developing a new set of axioms for Euclidean geometry, took as an axiom that the diagonal points of any quadrangle are never collinear. This is called Fano's Axiom. A Fano subplane however violates Fano's Axiom. They really should be called Anti-Fano subplanes, but this name change has not had many supporters.

In finite desarguesian planes, PG(2,q), Fano subplanes exist if and only if q is even (that is, a power of 2). The situation in non-desarguesian planes is unsettled. They could exist in any non-desarguesian plane of order greater than 6, and indeed, they have been found in all non-desarguesian planes in which they have been looked for (in both odd and even orders).

An open question is: Does every non-desarguesian plane contain a Fano subplane?

A theorem concerning Fano subplanes due to (Gleason 1956) is:

If every quadrangle in a finite projective plane has collinear diagonal points, then the plane is desarguesian (of even order).

Affine planes[edit]

Projectivization of the Euclidean plane produced the real projective plane. The inverse operation — starting with a projective plane, remove one line and all the points incident with that line — produces an affine plane.

Definition[edit]

More formally an affine plane consists of a set of lines and a set of points, and a relation between points and lines called incidence, having the following properties:

The second condition means that there are parallel lines and is known as Playfair's axiom. The expression "does not meet" in this condition is shorthand for "there does not exist a point incident with both lines."

The Euclidean plane and the Moulton plane are examples of infinite affine planes. A finite projective plane will produce a finite affine plane when one of its lines and the points on it are removed. The order of a finite affine plane is the number of points on any of its lines (this will be the same number as the order of the projective plane from which it comes). The affine planes which arise from the projective planes PG(2,q) are denoted by AG(2,q).

There is a projective plane of order N if and only if there is an affine plane of order N. When there is only one affine plane of order N there is only one projective plane of order N, but the converse is not true. The affine planes formed by the removal of different lines of the projective plane will be isomorphic if and only if the removed lines are in the same orbit of the collineation group of the projective plane. These statements hold for infinite projective planes as well.

Construction of projective planes from affine planes[edit]

The affine plane K² over K embeds into KP² via the map which sends affine (non-homogeneous) coordinates to homogeneous coordinates,

The complement of the image