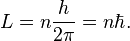Schrödinger equation

For a more general introduction to the topic, see Introduction to quantum mechanics.

Quantum mechanics
Uncertainty principle
Introduction Glossary History
Background[show]
Fundamentals[show]
Experiments[show]
Formulations[show]
Equations[hide] Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations[show]
Advanced topics[show]
Scientists[show]
v t e

 

In quantum mechanics, the Schrödinger equation is a partial differential equation that describes how the quantum state of a quantum system changes with time. It was formulated in late 1925, and published in 1926, by the Austrian physicist Erwin Schrödinger.^[1]

In classical mechanics Newton's second law, (F = ma), is used to mathematically predict what a given system will do at any time after a known initial condition. In quantum mechanics, the analogue of Newton's law is Schrödinger's equation for a quantum system (usually atoms, molecules, and subatomic particles whether free, bound, or localized). It is not a simple algebraic equation, but in general a linear partial differential equation, describing the time-evolution of the system's wave function (also called a "state function").^[2]:1–2

The concept of a wavefunction is a fundamental postulate of quantum mechanics. Although Schrödinger's equation is often presented as a separate postulate, some authors^{[3]:Chapter 3} show that some properties resulting from Schrödinger's equation may be deduced just from symmetry principles alone, for example the commutation relations. Generally, “derivations” of the Schrödinger equation demonstrate its mathematical plausibility for describing wave-particle duality, but to date there are no universally accepted derivations of Schrödinger's equation from appropriate axioms.

In the Copenhagen interpretation of quantum mechanics, the wave function is the most complete description that can be given of a physical system. Solutions to Schrödinger's equation describe not only molecular, atomic, and subatomic systems, but also macroscopic systems, possibly even the whole universe.^[4]:292ff The Schrödinger equation, in its most general form, is consistent with both classical mechanics and special relativity, but the original formulation by Schrödinger himself was non-relativistic.

The Schrödinger equation is not the only way to make predictions in quantum mechanics—other formulations can be used, such as Werner Heisenberg's matrix mechanics, and Richard Feynman's path integral formulation.

Equation

Time-dependent equation

The form of the Schrödinger equation depends on the physical situation (see below for special cases). The most general form is the time-dependent Schrödinger equation, which gives a description of a system evolving with time:^[5]:143

 

Time-dependent Schrödinger equation (general)

where i is the imaginary unit, ħ is the Planck constant divided by 2π, the symbol ∂/∂t indicates a partial derivative with respect to time t, Ψ (the Greek letter psi) is the wave function of the quantum system, and Ĥ is the Hamiltonian operator (which characterizes the total energy of any given wave function and takes different forms depending on the situation).

 

The most famous example is the non-relativistic Schrödinger equation for a single particle moving in an electric field (but not a magnetic field; see the Pauli equation):^[6]

Time-dependent Schrödinger equation (single non-relativistic particle)

where μ is the particle's "reduced mass", V is its potential energy, ∇² is the Laplacian (a differential operator), and Ψ is the wave function (more precisely, in this context, it is called the "position-space wave function"). In plain language, it means "total energy equals kinetic energy plus potential energy", but the terms take unfamiliar forms for reasons explained below.

Given the particular differential operators involved, this is a linear partial differential equation. It is also a diffusion equation, but unlike the heat equation, this one is also a wave equation given the imaginary unit present in the transient term.

The term "Schrödinger equation" can refer to both the general equation (first box above), or the specific nonrelativistic version (second box above and variations thereof). The general equation is indeed quite general, used throughout quantum mechanics, for everything from the Dirac equation to quantum field theory, by plugging in various complicated expressions for the Hamiltonian. The specific nonrelativistic version is a simplified approximation to reality, which is quite accurate in many situations, but very inaccurate in others (see relativistic quantum mechanics and relativistic quantum field theory).

To apply the Schrödinger equation, the Hamiltonian operator is set up for the system, accounting for the kinetic and potential energy of the particles constituting the system, then inserted into the Schrödinger equation. The resulting partial differential equation is solved for the wave function, which contains information about the system.

Time-independent equation

The time-independent Schrödinger equation predicts that wave functions can form standing waves, called stationary states (also called "orbitals", as in atomic orbitals or molecular orbitals). These states are important in their own right, and if the stationary states are classified and understood, then it becomes easier to solve the time-dependent Schrödinger equation for any state. The time-independent Schrödinger equation is the equation describing stationary states. (It is only used when the Hamiltonian itself is not dependent on time. However, even in this case the total wave function still has a time dependency.)

Time-independent Schrödinger equation (general)

In words, the equation states:

When the Hamiltonian operator acts on a certain wave function Ψ, and the result is proportional to the same wave function Ψ, then Ψ is a stationary state, and the proportionality constant, E, is the energy of the state Ψ.

The time-independent Schrödinger equation is discussed further below. In linear algebra terminology, this equation is an eigenvalue equation.

As before, the most famous manifestation is the non-relativistic Schrödinger equation for a single particle moving in an electric field (but not a magnetic field):

Time-independent Schrödinger equation (single non-relativistic particle)

with definitions as above.

Implications

The Schrödinger equation and its solutions introduced a breakthrough in thinking about physics. Schrödinger's equation was the first of its type, and solutions led to consequences that were very unusual and unexpected for the time.

Total, kinetic, and potential energy

The overall form of the equation is not unusual or unexpected as it uses the principle of the conservation of energy. The terms of the nonrelativistic Schrödinger equation can be interpreted as total energy of the system, equal to the system kinetic energy plus the system potential energy. In this respect, it is just the same as in classical physics.

Quantization

The Schrödinger equation predicts that if certain properties of a system are measured, the result may be quantized, meaning that only specific discrete values can occur. One example is energy quantization: the energy of an electron in an atom is always one of the quantized energy levels, a fact discovered via atomic spectroscopy. (Energy quantization is discussed below.) Another example is quantization of angular momentum. This was an assumption in the earlier Bohr model of the atom, but it is a prediction of the Schrödinger equation.

Another result of the Schrödinger equation is that not every measurement gives a quantized result in quantum mechanics. For example, position, momentum, time, and (in some situations) energy can have any value across a continuous range.^{[7]:165–167}

Measurement and uncertainty

In classical mechanics, a particle has, at every moment, an exact position and an exact momentum. These values change deterministically as the particle moves according to Newton's laws. Under the Copenhagen interpretation of quantum mechanics, particles do not have exactly determined properties, and when they are measured, the result is randomly drawn from a probability distribution. The Schrödinger equation predicts what the probability distributions are, but fundamentally cannot predict the exact result of each measurement.

The Heisenberg uncertainty principle is the statement of the inherent measurement uncertainty in quantum mechanics. It states that the more precisely a particle's position is known, the less precisely its momentum is known, and vice versa.

The Schrödinger equation describes the (deterministic) evolution of the wave function of a particle. However, even if the wave function is known exactly, the result of a specific measurement on the wave function is uncertain.

Quantum tunneling

 

In classical physics, when a ball is rolled slowly up a large hill, it will come to a stop and roll back, because it doesn't have enough energy to get over the top of the hill to the other side. However, the Schrödinger equation predicts that there is a small probability that the ball will get to the other side of the hill, even if it has too little energy to reach the top. This is called quantum tunneling. It is related to the distribution of energy: although the ball's assumed position seems to be on one side of the hill, there is a chance of finding it on the other side.

Particles as waves

 

The nonrelativistic Schrödinger equation is a type of partial differential equation called a wave equation. Therefore, it is often said particles can exhibit behavior usually attributed to waves. In some modern interpretations this description is reversed – the quantum state, i.e. wave, is the only genuine physical reality, and under the appropriate conditions it can show features of particle-like behavior. However, Ballentine ^{[3]:Chapter 4, p.99} shows that such an interpretation has problems. Ballentine points out that whilst it is arguable to associate a physical wave with a single particle, there is still only one Schrödinger wave equation for many particles. He points out:

"If a physical wave field were associated with a particle, or if a particle were identified with a wave packet, then corresponding to N interacting particles there should be N interacting waves in ordinary three-dimensional space. But according to (4.6) that is not the case; instead there is one "wave" function in an abstract 3N-dimensional configuration space. The misinterpretation of psi as a physical wave in ordinary space is possible only because the most common applications of quantum mechanics are to one-particle states, for which configuration space and ordinary space are isomorphic."

Two-slit diffraction is a famous example of the strange behaviors that waves regularly display, that are not intuitively associated with particles. The overlapping waves from the two slits cancel each other out in some locations, and reinforce each other in other locations, causing a complex pattern to emerge. Intuitively, one would not expect this pattern from firing a single particle at the slits, because the particle should pass through one slit or the other, not a complex overlap of both.

However, since the Schrödinger equation is a wave equation, a single particle fired through a double-slit does show this same pattern (figure on right). Note: The experiment must be repeated many times for the complex pattern to emerge. Although this is counterintuitive, the prediction is correct; in particular, electron diffraction and neutron diffraction are well understood and widely used in science and engineering.

Related to diffraction, particles also display superposition and interference.

The superposition property allows the particle to be in a quantum superposition of two or more quantum states at the same time. However, it is noted that a "quantum state" in QM means the probability that a system will be, for example at a position x, not that the system will actually be at position x. It does not infer that the particle itself may be in two classical states at once. Indeed, QM is generally unable to assign values for properties prior to measurement at all.

Interpretation of the wave function

The Schrödinger equation provides a way to calculate the wave function of a system and how it changes dynamically in time. However, the Schrödinger equation does not directly say what, exactly, the wave function is. Interpretations of quantum mechanics address questions such as what the relation is between the wave function, the underlying reality, and the results of experimental measurements.

An important aspect is the relationship between the Schrödinger equation and wavefunction collapse. In the oldest Copenhagen interpretation, particles follow the Schrödinger equation except during wavefunction collapse, during which they behave entirely differently. The advent of quantum decoherence theory allowed alternative approaches (such as the Everett many-worlds interpretation and consistent histories), wherein the Schrödinger equation is always satisfied, and wavefunction collapse should be explained as a consequence of the Schrödinger equation.

Historical background and development

 

Following Max Planck's quantization of light (see black body radiation), Albert Einstein interpreted Planck's quanta to be photons, particles of light, and proposed that the energy of a photon is proportional to its frequency, one of the first signs of wave–particle duality. Since energy and momentum are related in the same way as frequency and wavenumber in special relativity, it followed that the momentum p of a photon is inversely proportional to its wavelength λ, or proportional to its wavenumber k.

where h is Planck's constant. Louis de Broglie hypothesized that this is true for all particles, even particles which have mass such as electrons. He showed that, assuming that the matter waves propagate along with their particle counterparts, electrons form standing waves, meaning that only certain discrete rotational frequencies about the nucleus of an atom are allowed.^[8] These quantized orbits correspond to discrete energy levels, and de Broglie reproduced the Bohr model formula for the energy levels. The Bohr model was based on the assumed quantization of angular momentum L according to:

According to de Broglie the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron's orbit:

This approach essentially confined the electron wave in one dimension, along a circular orbit of radius r.

In 1921, prior to de Broglie, Arthur C. Lunn at the University of Chicago had used the same argument based on the completion of the relativistic energy–momentum 4-vector to derive what we now call the de Broglie relation.^[9] Unlike de Broglie, Lunn went on to formulate the differential equation now known as the Schrödinger equation, and solve for its energy eigenvalues for the hydrogen atom. Unfortunately the paper was rejected by the Physical Review, as recounted by Kamen.^[10]

Following up on de Broglie's ideas, physicist Peter Debye made an offhand comment that if particles behaved as waves, they should satisfy some sort of wave equation. Inspired by Debye's remark, Schrödinger decided to find a proper 3-dimensional wave equation for the electron. He was guided by William R. Hamilton's analogy between m