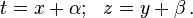Homogeneous differential equation
Homogeneous differential equation
A differential equation can be homogeneous in either of two respects: the coefficients of the differential terms in the first order case could behomogeneous functions of the variables, or for the linear case of any order there could be no constant term.
Contents
[hide]
Homogeneous type of first-order differential equations[edit]
| Differential equations |
|---|

Navier–Stokes differential equations used to simulate airflow around an obstruction.
|
| Classification |
| Solution |
A first-order ordinary differential equation in the form:
is a homogeneous type if both functions M(x, y) and N(x, y) are homogeneous functions of the same degree n.[1] That is, multiplying each variable by a parameter 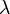 , we find
, we find
 and
and 
Thus,
Solution method[edit]
In the quotient  , we can let
, we can let 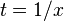 to simplify this quotient to a function
to simplify this quotient to a function 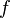 of the single variable
of the single variable 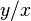 :
:
Introduce the change of variables  ; differentiate using the product rule:
; differentiate using the product rule:
thus transforming the original differential equation into the separable form
this form can now be integrated directly (see ordinary differential equation).
The equations in this discussion are not to be used as formulary for solutions; they are shown just to demonstrate the method of solution.
Special case[edit]
A first order differential equation of the form (a, b, c, e, f, g are all constants)
where af ≠ be can be transformed into a homogeneous type by a linear transformation of both variables ( and
and 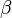 are constants):
are constants):
Homogeneous linear differential equations[edit]
Definition. A linear differential equation is called homogeneous if the following condition is satisfied: If 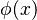 is a solution, so is
is a solution, so is  , where
, where  is an arbitrary (non-zero) constant. Note that in order for this condition to hold, each term in a linear differential equation of the dependent variable y must contain y or any derivative of y. A linear differential equation that fails this condition is called inhomogeneous.
is an arbitrary (non-zero) constant. Note that in order for this condition to hold, each term in a linear differential equation of the dependent variable y must contain y or any derivative of y. A linear differential equation that fails this condition is called inhomogeneous.
A linear differential equation can be represented as a linear operator acting on y(x) where x is usually the independent variable and y is the dependent variable. Therefore, the general form of a linear homogeneous differential equation is
where L is a differential operator, a sum of derivatives (defining the "0th derivative" as the original, non-differentiated function), each multiplied by a function  of x:
of x:
where  may be constants, but not all
may be constants, but not all  may be zero.
may be zero.
For example, the following differential equation is homogeneous:
whereas the following two are inhomogeneous:
It should be noted that the existence of a constant term is a sufficient condition for an equation to be inhomogeneous, as in the above example.
See also[edit]
Notes[edit]
References[edit]
- Boyce, William E.; DiPrima, Richard C. (2012), Elementary differential equations and boundary value problems (10th ed.), Wiley, ISBN 978-0470458310. (This is a good introductory reference on differential equations.)
- Ince, E. L. (1956), Ordinary differential equations, New York: Dover Publications, ISBN 0486603490. (This is a classic reference on ODEs, first published in 1926.)