Quantuum wave particle function
Quantuum wave particle function
Wave function
A wave function in quantum mechanics is a mathematical object that represents a particular pure quantum state of a specific isolated system of one or more particles. It is a central entity in quantum mechanics. The most common symbols for a wave function are the Greek letters ψ or Ψ (lower-case and capital psi).
A single wave function describes the entire system, covering at once all the particles in it. For the one state, however, there are many different wave functions, each giving its respective version, or representative[1] description, in a chosen coordinate system. Each of the different representatives encodes all observable items of information about the state, for example the average momentum of a particle, the different versions being mutually interconvertible by one-to-one mathematical transformations. In general, a physical observation of a quantum system in a particular state gives a partly unpredictable result. The wave function, however, encodes probabilities of the possible results, through mathematical operators called observables. Each of the many possible modes of physical observation is encoded by its own mathematical observable. Each such observable generates a representation that encompasses all the possible particular states of the specific system. For a particular state and coordinate system, for each representation there is just one representative wave function.
In non-relativistic quantum mechanics, disregarding spin, wave functions are solutions of the Schrödinger equation for the specific system, in a chosen representation, and coordinate system. This equation governs their dynamical behavior over time. Because the Schrödinger equation is mathematically a wave equation, a wave function behaves in some respects like other waves, such as water waves or waves on a string. This explains the name "wave function". The wave of the wave function, however, is not a wave in ordinary physical space; it is a wave in an abstract mathematical "space", known as "configuration space", and in this respect it differs fundamentally from water waves or waves on a string.[2][3][4][5][6][7][8]
The unit of measurement for ψ depends on the system, and can be found by dimensional analysis of the normalization condition for the system. For one particle in three dimensions, its units are [length]−3/2, because an integral of | ψ |2 over a region of three-dimensional space is a dimensionless probability.[9]
Contents
- 1 General introductory account
- 2 Historical background
- 3 Wave functions and function spaces
- 4 Definition (one spinless particle in 1d)
- 5 Definitions (other cases)
- 6 Inner product
- 7 Units of the wave function
- 8 More on wave functions and abstract state space
- 9 Position representations
- 10 Ontology
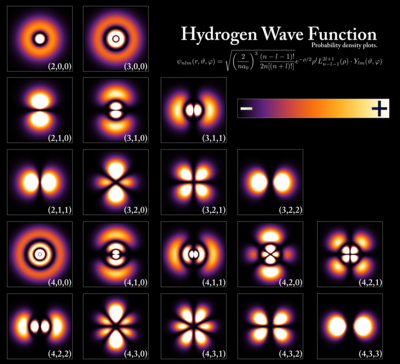
- 11 Examples
- 12 See also
- 13 Remarks
- 14 Notes
- 15 References
- 16 Further reading
- 17 External links
General introductory account
The present introductory account is initially confined to non-relativistic quantum mechanics, disregarding spin.
Representations
For a specific physical system, there are many possible alternative representations. Each representation covers at once all possible particular states of the specific system. The many representations give alternative ways of seeing the same ground, from different viewpoints.
Each representation is characterized by its generalized quantum configuration space, that is, its set of physical degrees of freedom, for example position, momentum, or spin, that jointly just exhaustively describe the system. Further, for the degrees of freedom, there are many suitable coordinate systems, continuous as well as discrete. Both representation and coordinate system may be freely chosen by the investigator.
In a chosen representation and coordinate system, a particular quantum state has one representative wave function. As a function, its domain is the generalized quantum configuration space. For systems without spin, its codomain is the set of complex numbers. Its values evolve in time, as precisely determined by the Schrödinger equation of the system.
A representation is mathematically formulated in a complete set of commuting observables,[nb 1][nb 2] sometimes referred to as a "maximum observation",[nb 3] or "maximal set of commuting observables".[10] The observables express the physical degrees of freedom, or generalized configuration space, of the representation. Mathematically, an observable is a Hermitian linear operator that transforms a state vector, or a wave function, as the case may be, so as to make it ready to supply probabilities of values of detected physical observables. For a representation, quantum mechanics requires that all the defining observables must commute, meaning that they can, in principle, simultaneously or jointly, be physically observed with arbitrary precision; thus the term simultaneous eigenstate. There is at least one representation for which the state is a simultaneous eigenstate.[nb 4][nb 5][nb 6][nb 7][nb 8][nb 9] The choice of representation restricts what can be precisely expressed about the state of the system. This is a characteristic feature of quantum mechanics as different from classical mechanics. For example, the position representation allows precise statement of the values of the position degrees of freedom, but is incompatible with precise statement of the values of the momentum degrees of freedom.
Transformation theory
For a specific quantum system, the many representations are mathematically interconvertible. Just as in classical mechanics, canonical transformations may be used for such interconversions. An example of a representation is the position coordinates of the particles over position space. Another example is the momenta of all the particles over momentum space. The two are related by a Fourier transform. Though these two representations are important, there are many others.
Vector characteristics
State vectors for a specific system can be added together and multiplied by complex numbers to form new state vectors, as they are elements of a vector space. This is the superposition principle of quantum mechanics. As constructs from state vectors, wave functions inherit this property. As solutions of their Schrödinger equation, they have it because that equation is linear. Wave functions for a specific system, in a chosen representation and coordinate system, can be added together and multiplied by complex numbers, and thus also form a vector space, which is recognizable as a function space. As a vector space, it also has an inner product which induces a metric. This makes it a complete metric topological space, indeed another Hilbert space. The inner product is a measure of the overlap between physical states and is used in the foundational probabilistic interpretation of quantum mechanics, the Born rule, relating transition probabilities to inner products. As a function space, its domain is the set of values of the degrees of freedom. Its range is the set of complex numbers.
Born's statistical interpretation
In Born's statistical interpretation,[11][12][13] the squared modulus of the wave function, | Ψ(·) |2, is a real number interpreted as the probability density, in a "measurement", of a system's being detected in a given configuration. A single-particle system's configuration could be as in a given position, or as having a given momentum, and possibly as having definite values for discrete degrees of freedom. The integral of this quantity, over all the system's degrees of freedom, must be 1 in accordance with the probability interpretation, this general requirement a wave function must satisfy is called the normalization condition. Since the wave function is complex valued, only its relative phase and relative magnitude can be measured. Its value does not in isolation tell anything about the magnitudes or directions of measurable observables; one has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function Ψ(·) and calculate the statistical distributions for measurable quantities.
Spin
Many kinds of particle, such as electrons and photons, have nonzero spin, and their wave functions must include this fundamental property as an intrinsic discrete degree of freedom. In general, for a particle with half-integer spin the wave function is a spinor, for a particle with integer spin the wave function is a tensor. Particles with spin zero are called scalar particles, those with spin 1 vector particles, and more generally for higher integer spin, tensor particles. The terminology derives from how the wave functions transform under a rotation of the coordinate system. No elementary particle with spin 3⁄2 or higher is known, except for the hypothesized spin 2 graviton. Other discrete variables can be included, such as isospin. When a system has internal degrees of freedom, the wave function at each point in the continuous degrees of freedom (e.g. a point in space) assigns a complex number for each possible value of the discrete degrees of freedom (e.g. z-component of spin). These values are often displayed in a column matrix (e.g. a 2 × 1 column vector for a non-relativistic electron with spin 1⁄2).
Quantum states and Schrödinger wave functions
There are two traditional mathematical formulations of the quantum state of a system, the Schrödinger way in terms of wave functions and the abstract way, originally primarily due to Dirac.[14] The Schrödinger way is in terms of functions of multiple real variables, such as Ψ(·), I. e wave functions. The abstract way is in terms of vectors, known as state vectors, that are elements of an abstract space for the specific system, the species of interest.[15] The abstract way is a generalization of the Schrödinger wave functions to abstract Hilbert space. Any Schrödinger formulation corresponds to a choice of representation. For general theory, the abstract way is often convenient. For specific problems, the Schrödinger way is often convenient.[nb 10] The link between abstract quantum states and wave functions is outlined below.
A choice of representation and coordinate system (e.g. Cartesian coordinates or spherical coordinates) in abstract Hilbert space allows for every state being expressed in terms of that choice. In practice, the wave function Ψ(ξ) (Schrödinger representation) is expressed as the inner product
where
is a basis element representing the precise state in which ξ has a precise value. The argument is thought of as variable over the complete domain of a representation. This means that ξ can take on all possible values of a complete set of observables, ξ = (χ1, χ2, …, χn, σ1, σ2, …, σs). The χi are, for notational purposes, thought of as continuously variable and the σi as discrete variables. The state vector
is representing a given quantum state under consideration. The time-dependence of states and wave functions is not made explicit here.
For definiteness, let ξ = (x, y, z, σz) be position in space and spin z-component of a single particle. Then
is a state in which the particle is located at (x, y, z) and has the definite value spin z-projection σz, and
is the wave function with the interpretation of a probability amplitude.
The procedure outlined here is analogous to expressing an ordinary vector in three-dimensional space in terms of components relative to a set of basis vectors. In that case, the components of a vector r = (rx, ry, rz) in terms of the ordinary basis is expressed as the dot product rx = ex ⋅ r, etc. There are two differences. The state vectors reside in a apace that is infinite-dimensional in general. In the example, for each triple (x, y, z) and each value of σz one has a component of Ψ. The other difference is that the inner product generally takes on complex values, whereas the dot product in three-dimensional space is real-valued.
Later, the Dirac bra–ket notation will sometimes be employed.
Historical background
| Quantum mechanics |
|---|

|
In 1905 Einstein postulated the proportionality between the frequency of a photon and its energy, E = hf,[16] and in 1916 the corresponding relation between photon momentum and wavelength, λ = h/p.[17] In 1923, De Broglie was the first to suggest that the relation λ = h/p, now called the De Broglie relation, holds for massive particles, the chief clue being Lorentz invariance,[18] and this can be viewed as the starting point for the modern development of quantum mechanics. The equations represent wave–particle duality for both massless and massive particles.
In the 1920s and 1930s, quantum mechanics was developed using calculus and linear algebra. Those who used the techniques of calculus included Louis de Broglie, Erwin Schrödinger, and others, developing "wave mechanics". Those who applied the methods of linear algebra included Werner Heisenberg, Max Born, and others, developing "matrix mechanics". Schrödinger subsequently showed that the two approaches were equivalent.[19]
In 1926, Schrödinger published the famous wave equation now named after him, indeed the Schrödinger equation, based on classical Conservation of energy using quantum operators and the de Broglie relations such that the solutions of the equation are the wave functions for the quantum system.[20] However, no one was clear on how to interpret it.[21] At first, Schrödinger and others thought that wave functions represent particles that are spread out with most of the particle being where the wave function is large.[22] This was shown to be incompatible with how elastic scattering of a wave packet representing a particle off a target appears; it spreads out in all directions.[11] While a scattered particle may scatter in any direction, it does not break up and take off in all directions. In 1926, Born provided the perspective of probability amplitude.[11][12][13][23] This relates calculations of quantum mechanics directly to probabilistic experimental observations. It is accepted as part of the Copenhagen interpretation of quantum mechanics. There are many other interpretations of quantum mechanics. In 1927, Hartree and Fock made the first step in an attempt to solve the N-body wave function, and developed the self-consistency cycle: an iterative algorithm to approximate the solution. Now it is also known as the Hartree–Fock method.[24] The Slater determinant and permanent (of a matrix) was part of the method, provided by John C. Slater.
Schrödinger did encounter an equation for the wave function that satisfied relativistic energy conservation before he published the non-relativistic one, but discarded it as it predicted negative probabilities and negative energies. In 1927, Klein, Gordon and Fock also found it, but incorporated the electromagnetic interaction and proved that it was Lorentz invariant. De Broglie also arrived at the same equation in 1928. This relativistic wave equation is now most commonly known as the Klein–Gordon equation.[25]
In 1927, Pauli phenomenologically found a non-relativistic equation to describe spin-1/2 particles in electromagnetic fields, now called the Pauli equation.[26] Pauli found the wave function was not described by a single complex function of space and time, but needed two complex numbers, which respectively correspond to the spin +1/2 and −1/2 states of the fermion. Soon after in 1928, Dirac found an equation from the first successful unification of special relativity and quantum mechanics applied to the electron, now called the Dirac equation. In this, the wave function is a spinor represented by four complex-valued components:[24] two for the electron and two for the electron's antiparticle, the positron. In the non-relativistic limit, the Dirac wave function resembles the Pauli wave function for the electron. Later, other relativistic wave equations were found.
Wave functions and wave equations in modern theories
All these wave equations are of enduring importance. The Schrödinger equation and the Pauli equation are under many circumstances excellent approximations of the relativistic variants. They are considerably easier to solve in practical problems than the relativistic equations. The Klein-Gordon equation and the Dirac equation, while being relativistic, do not represent full reconciliation of quantum mechanics and special relativity. The branch of quantum mechanics where these equations are studied the same way as the Schrödinger equation, often called relativistic quantum mechanics, while very successful, has its limitations (see e.g. Lamb shift) and conceptual problems (see e.g. Dirac sea).
Relativity makes it inevitable that the number of particles in a system is not constant. For full reconciliation, quantum field theory is needed.[27] In this theory, the wave equations and the wave functions have their place, but in a somewhat different guise. The main objects of interest are not the wave functions, but rather operators, so called field operators (or just fields where "operator" is understood) on the Hilbert space of states (to be described next section). It turns out that the original relativistic wave equations and their solutions are still needed to build the Hilbert space. Moreover, the free fields operators, i.e. when interactions are assumed not to exist, turn out to (formally) satisfy the same equation as do the fields (wave functions) in many cases.
Thus the Klein-Gordon equation (spin 0) and the Dirac equation (spin 1⁄2) in this guise remain in the theory. Higher spin analogues include the Proca equation (spin 1), Rarita–Schwinger equation (spin 3⁄2), and, more generally, the Bargmann–Wigner equations. For massless free fields two examples are the free field Maxwell equation (spin 1) and the free field Einstein equation (spin 2) for the field operators.[28] All of them are essentially a direct consequence of the requirement of Lorentz invariance. Their solutions must transform under Lorentz transformation in a prescribed way, i.e. under a particular representation of the Lorentz group and that together with few other reasonable demands, e.g. the cluster decomposition principle,[29] with implications for causality is enough to fix the equations.
It should be emphasized that this applies to free field equations; interactions are not included. It should also be noted that the equations and their solutions, though needed for the theories, are not the central objects of study.
Wave functions and function spaces
A wave function is by nature an element of a function space, indeed of several function spaces. A function space is a set of functions, usually with some defining requirements on the functions, together with a